Условие задачи
Двумерная случайная величина (X,Y) имеет равномерное распределение плотности вероятности в треугольной области ABC, заданное функцией f(x,y). Эта функция равна 1/S, если точка с координатами (х,у) принадлежит области ABC, и 0, если точка с координатами (х,у) не принадлежит данной области (S - площадь треугольника ABC с вершинами в точках А{0;0}, В{-2; 2}, С{-2; -2}).
Определить плотности распределения составляющей X - fx(x) и составляющей Y - fy(y), математические ожидания MX и MY, дисперсии DX и DY. Найти коэффициент корреляции случайных величин X и Y; установить, являются ли случайные величины независимыми.
Ответ
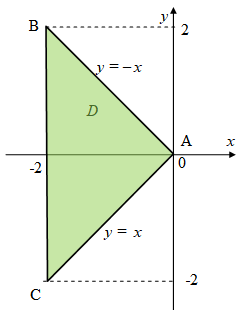
Площадь треугольника АВС равна S = 4 ед, тогда совместная плотность вероятности имеет вид:
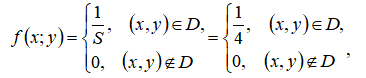
где D это треугольник АВС.
Плотности найдём по формулам:
