Условие задачи
Фирма производит два вида изделий, используя три вида ресурсов, и получает доход от реализации выпущенной продукции. Нормативы затрат ресурсов на единицу выпускаемой продукции, наличные объемы ресурсов и цены реализации продукции приведены в таблице.
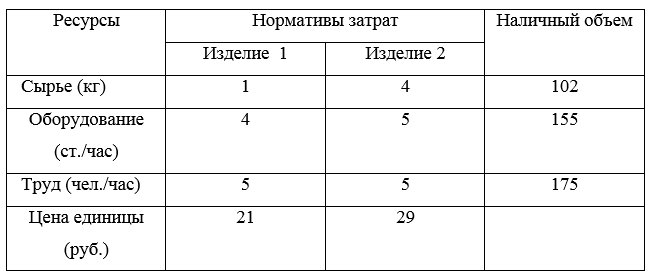
Задача фирмы состоит в том, чтобы определить программу выпуска, которая обеспечивает получение максимальной выручки от реализации готовой продукции.
Требуется:
1. Составить экономико-математическую модель расчета производственной программы и записать ее в виде задачи линейного программирования.
2. Найти графическим методом оптимальную программу выпуска продукции.
3. Составить двойственную задачу и с помощью условий "дополняющей нежесткости" определить оптимальные двойственные оценки ресурсов.
4. Привести экономическую интерпретацию переменных и оптимального решения двойственной задачи.
5. Найти интервалы устойчивости цен и с их помощью определить, изменится ли оптимальное решение задачи фирмы, если
а) цена изделия А возрастет на 20%,
б) цена изделия В уменьшится на 20%.
Ответ
1. Составим математическую модель задачи:
a. Введем переменные задачи:
х1- нормативы затрат изделия 1;
х2- нормативы затрат изделия 2.
b. Составим систему ограничений:
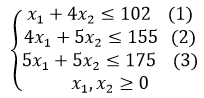
с. Зададим целевую фукцию:
F(x)=21x1+29x2max
2. Построим область допустимых решений
Для этого в прямоугольной системе координат построим прямую L1: x1+4x2=102, соответствующую ограничению (1). Для этого найдем координат...
