Функция задана таблицей своих значений. Найти многочлен не выше первой степени, аппроксимирующий функцию по методу наименьших квадратов. Найти значение многочлена в точке x = 2.57.
«Функция задана таблицей своих значений. Найти многочлен не выше первой степени, аппроксимирующий функцию по методу наименьших квадратов. Найти значение многочлена в точке x = 2.57.»
- Высшая математика
Условие:
Функция задана таблицей своих значений. Найти многочлен не выше первой степени, аппроксимирующий функцию по методу наименьших квадратов. Найти значение многочлена в точке x = 2.57. Изобразить точки таблицы и график аппроксимирующего многочлена на одном рисунке. Вычислить значение величины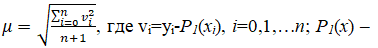 
аппроксимирующий многочлен. Величина μ оценивает близость аппроксимирующего многочлена к табличной функции.
Функция задана таблицей:
Решение:
Так как аппроксимирующий многочлен является многочленом не выше первой степени, то он может быть записан в виде: P1(x)=a1x+a0. Таким образом, система уравнений для нахождения a0 и a1 имеет вид:
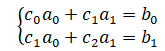
Для нахождения коэффициентов системы c0,c1,c2 и свободных членов системы b0 и b1 заполним следующую таблицу:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э