Исследовать функцию и построить от руки в декартовой системе координат её график с асимптотами (если такие имеются). На рисунке указать точки пересечения графика с осями координат, точки разрыва, экстремумов и перегибов.
- Высшая математика
Условие:
Исследовать функцию и построить от руки в декартовой системе координат её график с асимптотами (если такие имеются). На рисунке указать точки пересечения графика с осями координат, точки разрыва, экстремумов и перегибов.
Исследовать функцию необходимо по следующей схеме:
1. Найти область определения функции;
2. Исследовать функцию на чётность-нечётность;
3. Определить точки пересечения графика функции с осями координат;
4. Определить интервалы знакопостоянства функции (для ответа на вопрос – при каких значениях аргумента график функции располагается в верхней полуплоскости системы координат, а при каких в нижней);
5. Исследовать функцию на непрерывность, т.е. определить точки разрыва, характер разрыва и поведение функции в окрестности точек разрыва;
6. Исследовать функцию на наличие асимптот;
7. Исследовать функцию на возрастание и убывание;
8. Исследовать функцию на наличие экстремумов;
9. Исследовать функцию на выпуклость, вогнутость и наличие точек перегиба;
10. Построить график функции по результатам исследования.
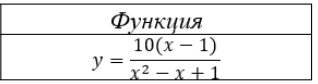
Решение:
1. Область определения функции: (-;+)
2. Исследуем функцию на чётность-нечётность:
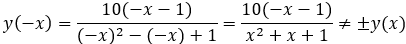
Функция ни четна, ни нечетна.
3. Определим точки пересечения графика функции с осями координат:
С осью Ох: y = 0
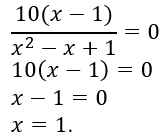
Получаем ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства