Из урны, содержащей 4 белых и 6 черных шаров, случайным образом без возвращения извлекается 2 шара. Случайная величина X - число белых шаров в выборке. Описать закон распределения, найти М(Х), D(X), σ(Х).

Случайная величина Х число белых шаров может принимать одно из 3-х значений: х = 0,1,2. Найдем вероятность каждого из этих значений.

Будем решать эту задачу с помощью классического определения вероятности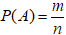
, где
n - количество всевозможных исходов.
m - количество благоприятных исходов.

Пусть событие А₀ из взятых наугад двух шаров нет белых шаров.

А₁ из взятых наугад 2 шаров один шар белый.

А2 из в...