Условие задачи
Известно, то время непрерывной работы электрической лампы есть случайная величина ξ (час), имеющая показательный закон распределения. Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины, если известно, что вероятность непрерывной работы лампы не менее 800 часов равна 0,2. Построить схематично графики функции распределения и функции плотности распределения этой случайной величины. Вычислить вероятность того, что выбранная случайным образом лампа непрерывно проработает:
а) не более 600 часов;
б) не менее 700 часов;
в) от 30 до 40 суток.
Ответ
Как известно, функция плотности распределения f(x) и функция распределения F(x) случайной величины , распределенной по показательному закону с параметром , имеют вид:
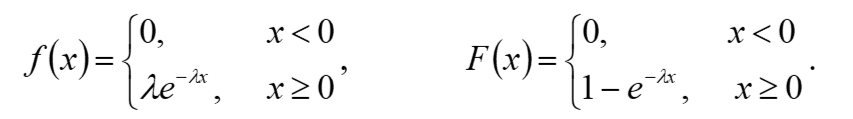
По условию задачи вероятность непрерывной работы лампы не менее 800 часов равна 0,2. Тогда получаем:
