Условие задачи
Известны результаты независимых наблюдений над случайной величиной Х.
1. Сгруппировать эти данные в интервальную таблицу, подобрав длину интервала.
2. Построить гистограмму, полигон частот и эмпирическую функцию распределения.
3. Найти несмещённые оценки для математического ожидания и дисперсии случайной величины Х. Указать моду М0.
4. По критерию χ2 (Пирсона) проверить гипотезу о том, что случайная величина Х имеет нормальный закон распределения.
5. Найти интервальные оценки математического ожидания и дисперсии случайной величины Х с уровнем доверия γ=0,9.
550; 551; 551; 550; 551; 562; 562; 551; 530; 542; 535; 542; 537; 543; 540; 556; 546; 556; 534; 548; 533; 558; 560; 558; 548; 541; 551; 549; 551; 550; 552; 568; 538; 551; 547; 552; 559; 557; 546; 552; 550; 557; 547; 552; 554; 547; 554; 567; 558; 563; 563; 562; 569; 552; 554; 549; 534; 566; 537; 550.
Ответ
1) Ранжируем ряд:
530; 533; 534; 534; 535; 537; 537; 538; 540; 541; 542; 542; 543; 546; 546; 547; 547; 547; 548; 548; 549; 549; 550; 550; 550; 550; 550; 551; 551; 551; 551; 551; 551; 551; 552; 552; 552; 552; 552; 554; 554; 554; 556; 556; 557; 557; 558; 558; 558; 559; 560; 562; 562; 562; 563; 563; 566; 567; 568; 569.
Найдем оптимальное число интервалов:
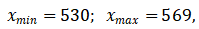следовательно, размах вариации
