Какие из нижеперечисленных векторов образуют ортонормированный базис в пространстве R^3. Какие из нижеперечисленных векторов образуют ортонормированный базис в пространстве R^3
«Какие из нижеперечисленных векторов образуют ортонормированный базис в пространстве R^3. Какие из нижеперечисленных векторов образуют ортонормированный базис в пространстве R^3»
- Высшая математика
Условие:
Какие из нижеперечисленных векторов образуют ортонормированный базис в пространстве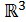 
:
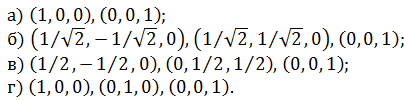
Решение:
Чтобы система векторов образовывала ортонормированный базис она, во-первых, должна быть базисом, во-вторых её векторы должны быть попарно ортогональны и в-третьих векторы должны иметь длину 1 (быть нормированными).
а) Эти векторы не образуют базис, поскольку базис трёхмерного пространства содержит три вектора;
б) Имеем,
система линейно независима и, следовательно, является базисом,
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э