Условие задачи
Небольшая фабрика изготовляет два вида красок: для наружных (№1) и внутренних (№2) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1т соответствующих красок приведены в табл.
Изучение рынка сбыта показало, что суточный спрос на краску для внутренних работ (№2) никогда не превышает спрос на краску для наружных работ (№1) более чем на 1 т. Кроме того, установлено, что спрос на краску № 2 никогда не превышает 2 т в сутки.
Прибыль от реализации одной тонны красок № 1 равна 3 тыс. денежных единиц, а для краски № 2 – 2 тыс. ден. ед.
Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Ответ
Построим математическую модель данной задачи.
Целевая функция:
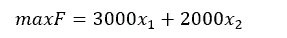
Ограничения:
