На линию связи поступает поток заявок на передачу речевых сообщений. Для организации речевой связи требуется 64 кбит/с. Пусть: λ — интенсивность поступления заявок, а 1/μ — среднее время их обслуживания.

           На линию связи поступает поток заявок на передачу речевых сообщений. Для организации речевой связи требуется 64 кбит/с. Пусть: λ — интенсивность поступления заявок, а 1/μ — среднее время их обслуживания. Варианты выбора входных параметров: λ = 1, 2, 3, 4 заявки за 3 минуты, 1/μ=3 минуты. Предположим, что поступление заявок подчиняется пуассоновскому закону, а время обслуживания имеет экспоненциальное распределение. Дать ответы на следующие вопросы:

          1. Найти минимальную скорость линии (число каналов  ), при котором доля потерянных заявок будет менее 0,1.

          2. Для найденного значения 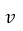 построить диаграмму переходов и выписать систему уравнений статистического равновесия.

          3. Найти вероятности стационарных состояний модели, вероятности потерь по времени, а также доли потерянных заявок и потерянного трафика. Далее, используя формулу Литтла, найти среднее число занятых каналов.

         4. Поступившая заявка получила отказ в обслуживании. Какова вероятность того, что следующим событием в системе будет поступление новой заявки? Какова для неё вероятность получить отказ в обслуживании?

         5. Найти функцию распределения времени до события, следующего после освобождения одного из   занятых каналов. Какова вероятность его осуществления?

6. Найти среднее время до освобождения всех каналов, если новые заявки не поступают.

         7. Определить доли времени, когда: а) все 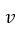 каналов будут свободны; б) будет занято не менее трёх каналов; в) будут свободными не менее двух каналов.