Найти частное решение дифференциального уравнения (линейное однородное дифференциальное уравнение с постоянными коэффициентами).
«Найти частное решение дифференциального уравнения (линейное однородное дифференциальное уравнение с постоянными коэффициентами).»
- Высшая математика
Условие:
Найти частное решение дифференциального уравнения y ″ − 2y ′ + y = 0 (1), удовлетворяющее начальным условиям y (0) = 4, y ′(0) = 2.
Решение:
Данное уравнение линейное однородное дифференциальное уравнение с постоянными коэффициентами. Для его решения составим характеристическое уравнение и найдем его корни
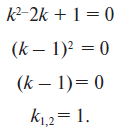
Так как корни действительные совпадающие, частные решения данного уравнения имеют вид y1 = ex и y2 = xex, а общее решение уравнения (1) запишется как
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э