Найти частное решение линейного неоднородного дифференциального уравнения 2-го порядка, удовлетворяющее начальным условиям.
«Найти частное решение линейного неоднородного дифференциального уравнения 2-го порядка, удовлетворяющее начальным условиям.»
- Высшая математика
Условие:
Найти частное решение линейного неоднородного дифференциального уравнения 2-го порядка, удовлетворяющее начальным условиям.
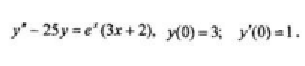
Решение:
r2 +0 r - 25 = 0
D=02 - 4∙1∙(-25)=100
Корни характеристического уравнения:
r1 = 5
r2 = -5
Следовательно, фундаментальную систему решений составляют функции:
y1 = e5x
y2 = e-5x
Общее решение однородного уравнения имеет вид:
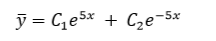
Ci R
Рассмотрим правую часть:
f(x) = (3∙x+2)∙ex
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = ex(P(x)cos(...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э