Найти множества АВ, АВ, А\В, В\А, АВ, Ā, С=(АВ)А, выяснить, какая из пяти возможностей выполнена для множеств, найти множество всех подмножеств множества В.
«Найти множества АВ, АВ, А\В, В\А, АВ, Ā, С=(АВ)А, выяснить, какая из пяти возможностей выполнена для множеств, найти множество всех подмножеств множества В.»
- Высшая математика
Условие:
Для универсального множества U = {-5,-4,-3,-2,-1, 1, 2, 3, 4, 5}, множества А, заданного списком и для В, являющимся множеством корней уравнения х4+aх3+bх2+gх+d=0
а) найти множества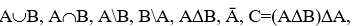
б) выяснить, какая из пяти возможностей выполнена для множеств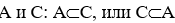 
или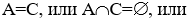 
А и С находятся в общем положении,
в) найти множество всех подмножеств множества В.
Решение:
Дано:
U={-5,-4,-3,-2,-1,1,2,3,4,5}
A={-1,1,2,3}
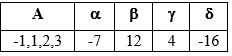
множество B является корнем уравнения:
x4-7x3+12x2+4x-16=0
Найти:
а) множества AB,AB,A\B,B\A,AB,A ̅,C=(AB)A
б) выяснить,какая из пяти возможностей выполнена для множества А и С:
AC,CA,A=C,AC= или А и С находнятся в общем положении
в) найти множество всех подмножеств множества В
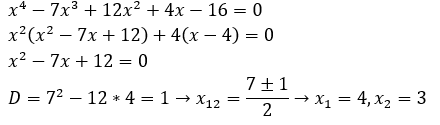
Получим:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э