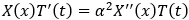Условие:
Найти распределение температуры в стержне длиной l с теплоизолированной боковой поверхностью, решив уравнение теплопроводности 
с заданными условиями на границах и начальным условием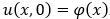 
.
Записать аналитическое решение. Построить приближенное графики распределения температуры в стержне в моменты времени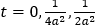 
, используя не менее четырех ненулевых слагаемых тригонометрического ряда, полученного в аналитическом решении. Изучить поведение u(x, t) при t →∞ . Построить графики частичных сумм тригонометрического ряда 
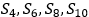в начальный момент времени и функцию φ(x).
Концы стержня теплоизолированы,
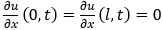
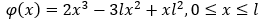
Решение:
Согласно методу Фурье ищем решение задачи в виде произведения двух функций:
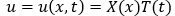
Где X(x) зависит только от x , а T(t) только от t.
Подставляем в уравнение:
