1. Главная
  2. Библиотека
  3. Высшая математика
  4. Для функции f(x)=2x2+4x a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX...

Для функции f(x)=2x2+4x a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

«Для функции f(x)=2x2+4x a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.»
  • Высшая математика

Условие:

Для функции f(x)=2x2+4x

a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой 2x+y−6=0. Напишите уравнение этой касательной.

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

Решение:

а)

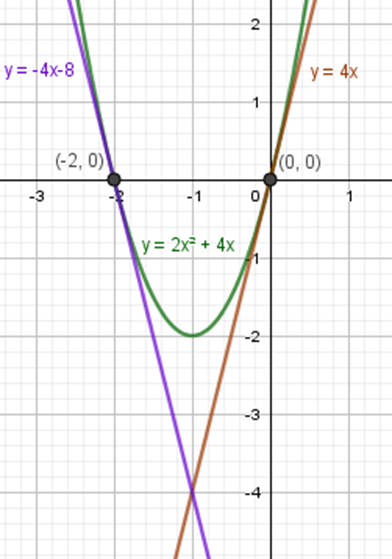
Находим точки пересечения, решаем уравнение:2x2+4x=02x(x+2)=0[x=0x=2

Две точки на оси: (0;0) и (-2;0).

Касательная в точке x0=0:

f(x0)=0, f(x)=4x+4f(x0)=40+4=4y=4(x0)+0=4x

Касательная в точке x0=2:

f(x0)=0, f(x)=4x+4f(x0)=4(2)+4=4y=4(x+2)+0=4x8

б)

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я