Условие задачи
Непрерывная случайная величина задана интегральной функцией распределения F(x). Требуется найти:
1) дифференциальную функцию распределения f(x) (плотность вероятности);
2) математическое ожидание M(X)
3) дисперсию D(X) и среднее квадратическое отклонение σ(X)
4) вероятность попадания заданной случайной величины X в заданный интервал P(α<X<β);
5) построить график интегральной функции распределения;
6) построить график дифференциальной функции распределения
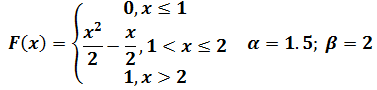
Ответ
1) Найдем плотность распределения вероятностей как производную от функции распределения:
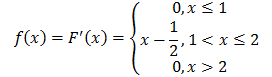
2) 3) Вычислим математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X:









