Ниже приведены комплексные задачи линейного программирования. Необходимо выполнить в указанном порядке следующие задания. 1. Найти оптимальный план задачи графическим методом.
- Высшая математика
Условие:
Ниже приведены комплексные задачи линейного программирования. Необходимо выполнить в указанном порядке следующие задания.
1. Найти оптимальный план задачи графическим методом.
2. Построить двойственную задачу.
3. Найти оптимальный план двойственной задачи из графического решения прямой задачи, используя условия дополняющей нежесткости.
4. Найти оптимальный план прямой задачи симплекс-методом (для построения исходного опорного плана рекомендуется использовать метод искусственного базиса).
5. Найти оптимальный план двойственной задачи по первой теореме двойственности, используя окончательную симплекс- таблицу, полученную при решении прямой задачи (п. 4). Проверить утверждение «значения целевых функций пары двойственных задач на своих оптимальных решениях совпадают».
6. Двойственную задачу решить симплекс-методом, затем, используя окончательную симплекс-таблицу двойственной задачи, найти оптимальный план прямой задачи по первой теореме двойственности. Сравнить результат с результатом, полученным графическим методом (п. 1).
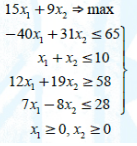
Решение:
1) Решим задачу графическим методом.
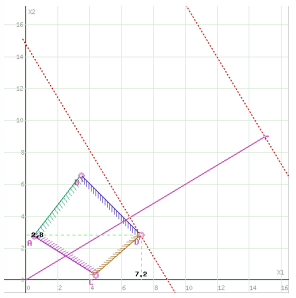
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области ...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства