Однородный груз сосредоточен в м пунктах отправления А1, А2,…,Ам и должен быть распределен между н получателей В1, В2,…,Вн. Составить математическую модель с учетом данных задания и определить возможность удовлетворения всех заявок имеющимися запасами.

Однородный груз сосредоточен в m пунктах отправления (на m складах) А₁, А₂,…,А_m и должен быть распределен между n получателей В₁, В₂,…,В_n. Пусть a_i – объём запаса груза в пункте 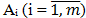, b_j – объём заявки в пункте  –  стоимость перевозки единицы груза из пункта А_i в пункт .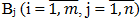

a.  Составить математическую модель с учетом данных задания и определить возможность удовлетворения всех заявок имеющимися запасами.

b. Определить начальный базисный план транспортной задачи методом северо-западного угла и указать стоимость перевозки груза по этому плану.

с. Определить начальный базисный план транспортной задачи методом наименьшей стоимости и указать стоимость перевозки груза по этому плану.

d. Составить план перевозки груза, учитывай запасы его в пунктах определения и заявки на этот груз в пунктах получения, и также обеспечивающий наименьшую возможную стоимость перевозки с учетом тарифной матрицы С. Оптимальный план вычислить методом потенциалов, взяв за начальный план один из  построенных выше.