Условие задачи
По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование строительных организаций региона по недельному объему выполненных строительных работ (тыс. руб.). Предполагая, что в регионе функционируют 1300 строительных организаций, получены следующие данные:
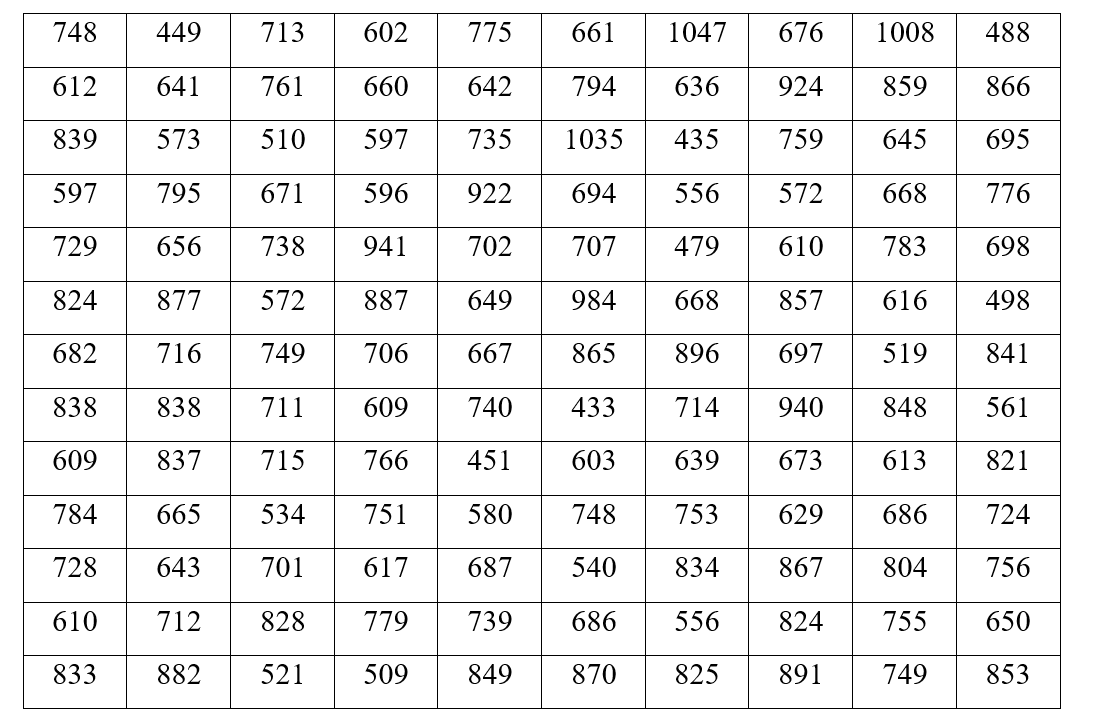
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.
По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
Найти:
а) границы, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организаций региона;
б) вероятность того, что доля всех строительных организаций, объем которых не менее 600 тыс. руб., отличается от доли таких организаций в выборке не более чем на 0,05 (по абсолютной величине);
в) объем бесповторной выборки, при котором те же границы для среднего объема выполненных работ (см. п. а)) можно гарантировать с вероятностью 0,9876.
Ответ
Выпишем элементы данной выборки в порядке их возрастания:
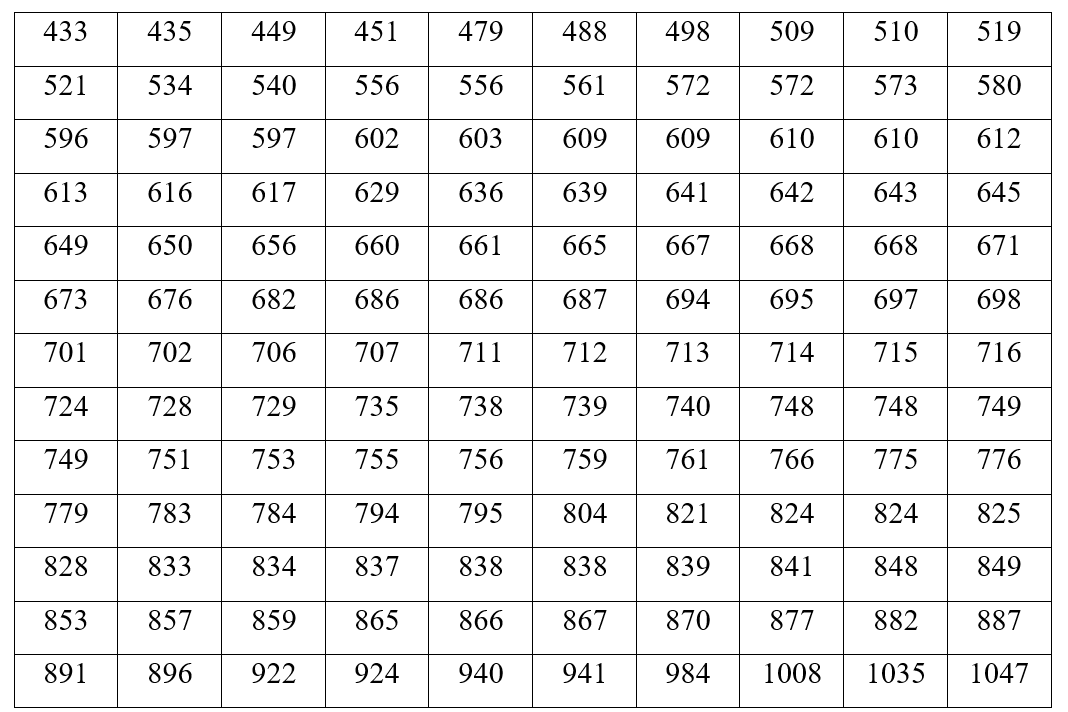
Объем выборки n=130. Для построения интервального вариационного ряда определим шаг выборки, воспользовавшись формулой Стерджесса:
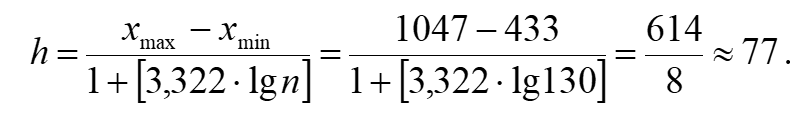
Нижняя граница...
