Условие задачи
Показать, что множество всех целых чисел (положительных, отрицательных и нуля) является группой по операциям:
а) обычного сложения G+,
б) обычного умножения Gх
В группе G+ по операции сложения выделить подгруппу, состоящую из чисел:
а) кратных 3,
б) кратных 4,
в) кратных 5.
Построить смежные классы для каждой из этих подгрупп.
Ответ
Покажем, что множество всех целых чисел удовлетворяет групповым аксиомам.
1. Замкнутость.
Операция суммирования или умножения для любых целых чисел дает также целое число, т.е. число из рассматриваемого множества.
2. Ассоциативность.
Для рассматриваемых операций результат не зависит от очередности выбора элементов нашего множества:
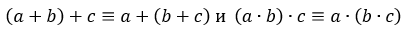
3. Наличие нулевого элемента
Для операции сложения это нуль а+0=а, а дл...
Потяни
