Предприятие выпускает два вида продукции A_1 и A_2, используя при этом три вида сырья S_1,S_2 и S_3. Известны запасы сырья равные b_1,b_2 и b_3 соответственно.
- Высшая математика
Условие:
Предприятие выпускает два вида продукции A1 и A2, используя при этом три вида сырья S1, S2 и S3 . Известны запасы сырья равные b1, b2 и b3 соответственно. Расход сырья вида Si на производство единицы продукции Aj равен ai,j . Доход от реализации единицы продукции Aj составляет cj , при котором доход будет максимальным. Решить задачу графическим методом; составить каноническую модель данной задачи и решить ее симплекс-методом. Найти двойственные оценки цен на сырье, из решения симметричной двойственной задачи.
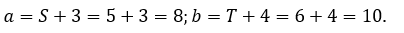
Запишем M – матрицу коэффициентов ai,j и B – матрицу запасов сырья bi.
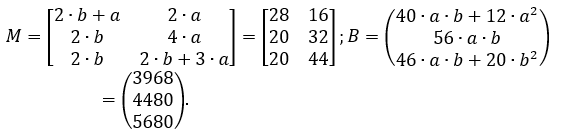
Коэффициенты функции цели 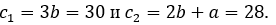
Математическая модель задачи
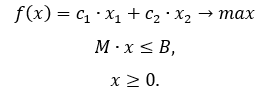
Решение:
Пусть x1 количество продукции A1 , ед.; x2 количество продукции A2 , ед. Подставим в математическую модель задачи числовые данные:

Решим задачу графическим методом. С учетом системы ограничений построим множество допустимых решений. Строим в системе координат прямые:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства