Главная
Библиотека
Высшая математика
Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Нормы расхода сырья, времени работы оборудования и...

Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Нормы расхода сырья, времени работы оборудования и затрат на электроэнергию

«Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Нормы расхода сырья, времени работы оборудования и затрат на электроэнергию»

16 августа 2024
Высшая математика

Условие:

Предприятие выпускает три вида крепежных изделий: гайки, болты и шайбы. Нормы расхода сырья, времени работы оборудования и затрат на электроэнергию, которые необходимы для производства одной тонны каждого изделия, приведены в таблице.

Месячные запасы ресурсов, которыми располагает предприятие, ограничены. По сырью эти ограничения обусловлены емкостью складских помещений, по оборудованию – станочным парком и трудовыми ресурсами, по электроэнергии – техническими и финансовыми причинами. Спрос на шайбы не превосходит 5/11 т, а спрос на гайки не превышает 11 т. Размеры запасов и прибыль от реализации продукции в у.е. за 1 тонну приведены в таблице.

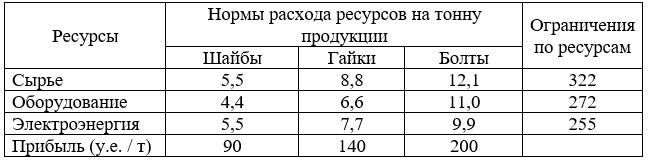
Требуется сформировать месячную производственную программу (определить объемы выпуска каждого вида продукции), при которой прибыль от реализации будет максимальной. Составить математическую модель данной задачи и решить её симплекс-методом.

Решение:

1. Составляем математическую модель нашей задачи.

Вводим обозначения для объемов выпуска каждого вида продукции:

x₁ месячная программа выпуска шайб (т);

x₂ месячная программа выпуска гаек (т);

x₃ месячная программа выпуска болтов (т).

При этом прибыль предприятия от реализации продукции составит

F = 90x₁ + 140x₂+ 200x₃ у.е.

Целью решения задачи является определение среди всех допустимых таких значений x₁, x₂ и x₃, которые максимизируют прибыль предприятия от реализации продукции.

Рассмотрим ограничения задачи.

Значения программы выпуска шайб, гаек и болтов не могут быть отрицательными, поэ...