Условие задачи
Предприятию необходимо перевезти со склада по железной дороге изделия трех различных видов. Изделий первого вида не более р1, изделий второго вида не более р2, изделий третьего вида не более р3.
Подразделение железной дороги для этой перевозки может выделить специально оборудованные вагоны 2 типов. Для полной загрузки вагона в него следует помещать изделия всех трех видов. При этом в вагон типа А входит а1 изделий первого типа, а2 изделий второго типа, а3 изделий третьего типа. В вагон типа В входит b1 изделий первого типа, b2 изделий второго типа, b3 изделий третьего типа.
Известно, что экономия от перевозки груза в вагоне типа А составляет α условных стоимостных единиц, а экономия от перевозки в вагоне типа В – β условных единиц.
Таблица 5. Данные о загрузке вагонов различными изделиями
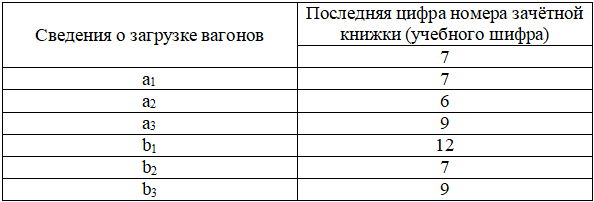
Таблица 6. Данные о наличии грузов на складе и экономия от перевозки
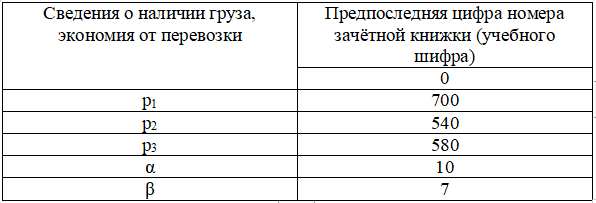
Сколько вагонов каждого типа следует выделить для перевозки, чтобы суммарная экономия от перевозки груза была наибольшая?
Ответ
Для составления математической модели задачи нужно знать, что является целевой функцией. Целевой функцией является суммарная экономия от перевозки, вернее ее максимальное значение:
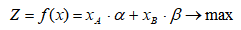
где Z суммарная экономия;
xА число вагонов типа А;
xВ число вагонов типа В;
a экономия от перевозки груза в вагоне типа А, усл. ед./ваг.;
b экономия от перевозки груза в вагоне типа В, усл. ед./ваг.
Разработаем систему огра...
