Условие задачи
Привести уравнение кривой второго порядка к каноническому виду: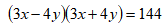 
. Для эллипса найти координаты вершин и фокусов, для гиперболы – координаты вершин, фокусов и уравнения асимптот, для параболы – координаты фокуса и уравнение директрисы, для окружности – координаты центра и радиус. Сделать чертеж.
Ответ
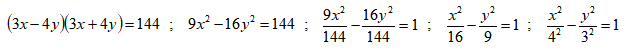
- каноническое уравнение гиперболы с действительной полуосью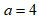 
, мнимой полуосью
Потяни
