Главная
Библиотека
Высшая математика
Производственное объединение состоит из четырех предприятий. Общая сумма капитальных вложений равна семьсот млн. руб., выд...

Производственное объединение состоит из четырех предприятий. Общая сумма капитальных вложений равна семьсот млн. руб., выделяемые предприятиям суммы кратны сто млн. руб. Если j-е предприятие получает инвестиции в объеме ξ млн. руб.,

«Производственное объединение состоит из четырех предприятий. Общая сумма капитальных вложений равна семьсот млн. руб., выделяемые предприятиям суммы кратны сто млн. руб. Если j-е предприятие получает инвестиции в объеме ξ млн. руб.,»

19 ноября 2024
Высшая математика

Условие:

Производственное объединение состоит из четырех предприятий. Общая сумма капитальных вложений равна 700 млн. руб., выделяемые предприятиям суммы кратны 100 млн. руб. Если j-е предприятие получает инвестиции в объеме ξ млн. руб., то прирост годовой прибыли на этом предприятии составит fj(ξ) млн. руб. в год. Значения функций fj(ξ) известны и для каждого варианта компактно записаны в таблице №2 в следующем виде:

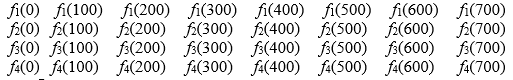
Требуется найти такое распределение инвестиций между предприятиями, которое максимизирует суммарный прирост прибыли на всех предприятиях вместе. Для этого необходимо составить математическую модель динамической задачи распределения инвестиций и решить ее методом динамического программирования, обосновывая каждый шаг вычислительного процесса.

Решение:

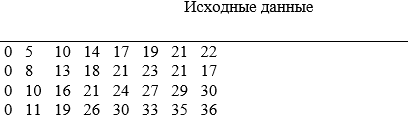
Запишем исходные данные в следующем виде:

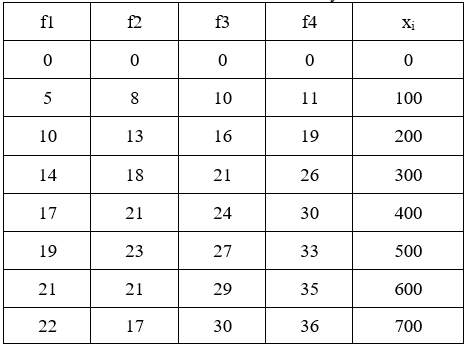
I этап. Условная оптимизация.

1-ый шаг. k = 4.

Предположим, что все средства в количестве x₄= 700 отданы предприятию №4. В этом случае, максимальный доход, как это видно из таблицы, составит f₄(u₄) = 36, следовательно, F₄(e₄) = f₄(u₄)