Условие задачи
Рассмотреть задачу целевого программирования, в которой множество допустимых решений задается неравенствами
x1 + 2x2 ≤ 4,4x1 + x2 ≤ 4 и x1,2 ≥ 0,
критерии заданы соотношениями
z1 = 2x1 + x2, z2 = 2x2,
а целевая точка совпадает с идеальной точкой z*, отклонение от которой задается функцией
ρ(z, z*) = max(z1* - z1), (z2* - z2).
Найти и изобразить множество достижимых критериальных векторов Z, его паретову границу P(Z) и идеальную точку z*. Изобразить линии уровня функции ρ(z, z*). Графически решить задачу нахождения достижимой точки (z1', z2'), дающей минимум отклонения от идеальной точки; аналитически записать задачу минимизации отклонения от идеальной точки в виде задачи линейного программирования.
Ответ
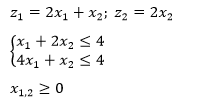
Множество допустимых решений имеет вид
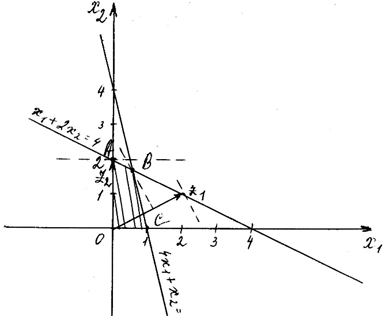
Найдем точки, оптимальные по критериям z1 и z2 в отдельности. Для этого построим векторы, имеющие направления векторов (2;1) и (0;2), и перпендикулярно им линии ...
