Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.
«Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.»
- Высшая математика
Условие:
Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.
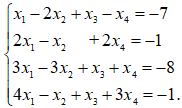
Решение:
Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем расширенную матрицу системы:
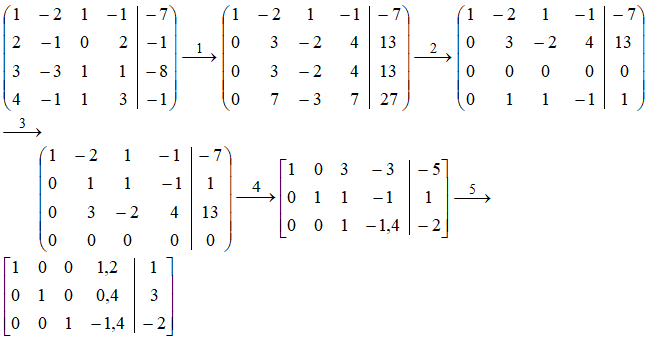
Поясним сделанные преобразования:
1. Первую строку умножим последовательно на (- 2), (-3), (-4) и приб...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э