Условие:
Решить смешанную задачу.
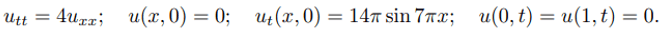
Решение:
utt=4u_xx;
u(x,0)=0,
ut (x,0)=14 sin7x,
u(0,t)=u(1,t)=0.
Для решения задачи (1) (3) применим метод Фурье разделения переменных. Ненулевое решение задачи ищем в виде
u(x,t)=X(x) ∙ T(t).
Подставим предполагаемую форму решения в исходное уравнение (1)
X(x)T''(t)=4X''(x)T(t)
Разделим равенство на 4X(x)∙T(t)(T''(t))/(4
T(t))=X''(x)/X(x) =-=const,
т.к. левая часть равенства зависит только от t, а правая только от x.
В результате переменные разделяются, и получается два обыкновенных дифференциальных линейных уравнения
T^'' (t)+4T(t)=0,
X''(x)+X(x)=0.
Подставляя u(x,t) в виде X(x)∙T(t) в граничные условия (3)...
