Условие:
С целью определения средней величины транспортных затрат (тыс. руб.) на доставку одной тонны продукции предприятия пищевой промышленности к потребителям в некотором крупном мегаполисе, имеющем 2750 предприятий, по схеме собственно-случайной бесповторной выборки проведено обследование 240 предприятий. Распределение транспортных затрат (тыс. руб.) представлено в таблице:
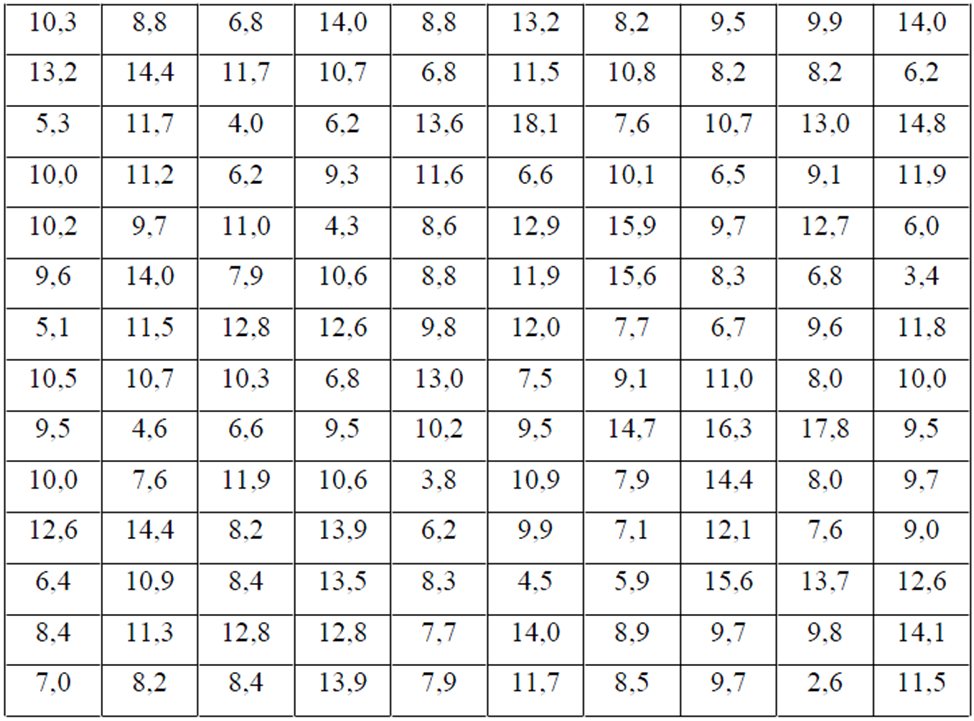
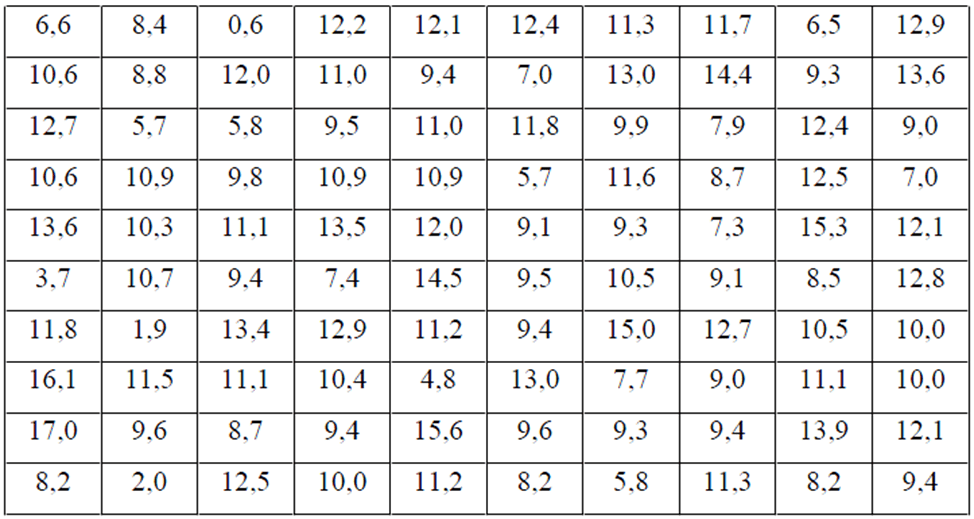
Составить интервальный вариационный ряд. Записать эмпирическую функцию распределения и построить ее график. На одном чертеже изобразить гистограмму и полигон частот.
По сгруппированным данным вычислить выборочные числовые характеристики: среднее арифметическое, исправленную выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию, эксцесс, моду и медиану.
Найти:
а) вероятность того, что средняя величина транспортных затрат предприятия отличается от полученной по выборке не более чем на 200 руб.;
б) границы, в которых с вероятностью 0,98 заключена доля всех предприятия, транспортные затраты которых составляют не менее 10 тыс. руб.;
в) объем бесповторной выборки, при котором границы для доли всех предприятий, полученные в п. б), можно гарантировать с вероятностью 0,95.
Решение:
Выпишем элементы данной выборки в порядке их возрастания:
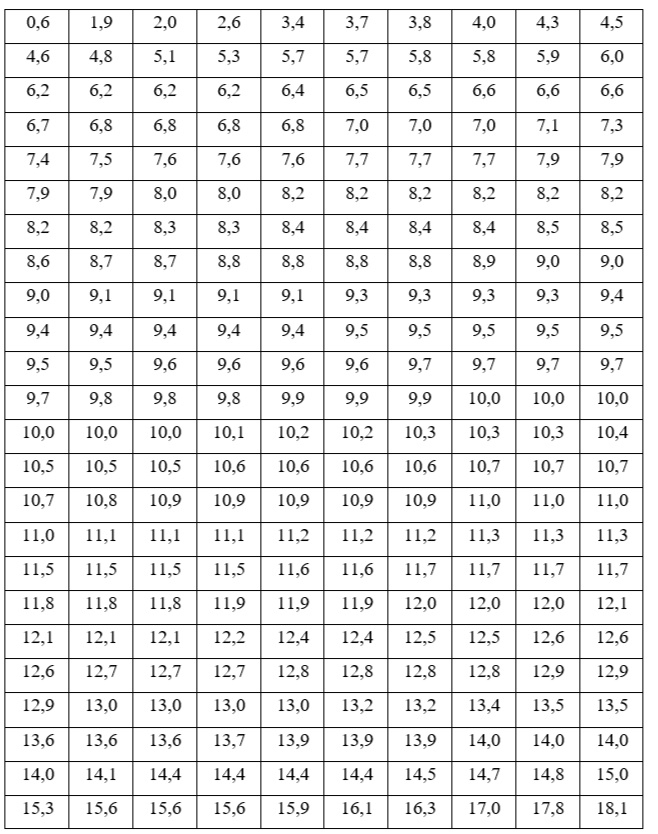
Объем выборки n=240. Для построения интервального вариационного ряда определим шаг выборки, воспользовавшись формулой Стерджесса:
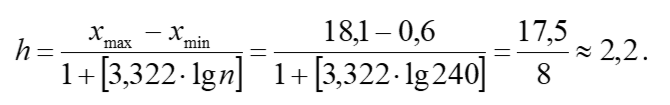
Нижняя граница...
