Условие задачи
С помощью преобразования координат привести данные алгебраические уравнения к каноническому виду и установить геометрический тип соответствующей линии; сделать чертёж.
1) 9x2 + 9y2 - 108y - 252 = 0
2) 10x2 + 4y2 - 200x - 24y -264 = 0
3) 9x2 - y2 - 180x - 18y +675 = 0
4) -3x2 + 20x - 5y - 130 = 0
Ответ
1) 9x2+ 9y2- 108y - 252 = 0
Выделим полные квадраты:
9x2 + 9(y2 - 12y + 36) - 325 - 252 = 0
9x2 + 9(y - 6)2 - 576 = 0
9x2 + 9(y - 6)2 = 576
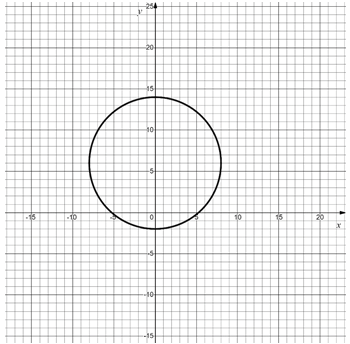
x2 + (y - 6)2 = 64
Данное уравнение определяет окружность с центром в точке C(0; 6). Сделаем чертеж:
2) 10x2+ 4y2- 200x - 24y -264 = 0
10(x2 - 20x) + 4(y2 -6y) - 264 = 0
10(x2 - 20x + 100) - 1000 + 4(y2 - 6y + 9) -36 -264 = 0
10(x -10)2 - 1000 +(y - 3)2 ...
Потяни
