Составить математическую модель и решить задачу симплексным методом. В производстве пользующихся спросом двух изделий (A и B) принимают участие 3 цеха фирмы.
- Высшая математика
Условие:
Составить математическую модель и решить задачу симплексным методом.
В производстве пользующихся спросом двух изделий (A и B) принимают участие 3 цеха фирмы. На изготовление одного изделия А 1-й цех затрачивает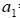 
= 8 ч, 2-й цех – 
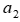= 7 ч, 3-й цех – 
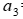=7 ч. На изготовление одного изделия В 1-й цех затрачивает 
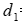=10 ч, 2-й цех – 
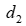=5 ч, 3-й цех – 
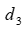=2ч. На производство обоих изделий 1-й цех может затратить не более 
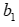=459 ч, 2-й цех – не более 
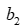=379 ч, 3-й цех – не более 
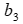=459ч.
От реализации одного изделия А фирма получает доход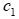 
= 9 рублей, изделия В – 
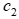= 9 рублей.
Определить максимальный доход от реализации всех изделий А и В.
Решение:
Введем данные в таблицу.
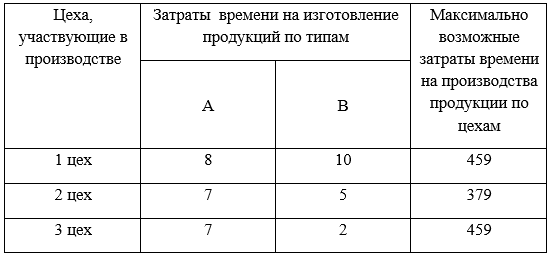
Для начала работы введем обозначения:
Пусть х1 количество продукции А, х2 - количество продукции В, производство которых дает наибольшую прибыль.
Учитывая величины дохода от реализации изделий А и изделий В, можно определить доход от реализации обеих продукций как 9х1 +9х2.
Тогда целевая функция для получения максимального дохода будет иметь следующий вид:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства