Условие задачи
Свести к интегральному уравнению краевую задачу:
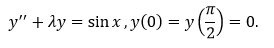
Ответ
Имеем уравнение вида:
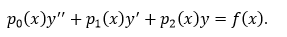
Построим вначале функцию Грина для краевой задачи:
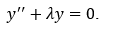
Покажем, что краевая задача имеет лишь тривиальное решениеy(x) 0.
Имеем:
👋 Решение задач
📚 Высшая математика
решение задачи на тему:
Дата добавления: 03.08.2024

Свести к интегральному уравнению краевую задачу:
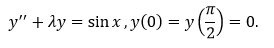
Ответ
Имеем уравнение вида:
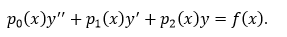
Построим вначале функцию Грина для краевой задачи:
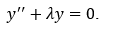
Покажем, что краевая задача имеет лишь тривиальное решениеy(x) 0.
Имеем:


Активируй безлимит с подпиской Кампус
Решай задачи без ограничений
 Материалы со всех ВУЗов страны
Материалы со всех ВУЗов страны
 2 000 000+ полезных материалов
2 000 000+ полезных материалов
 Это примеры на которых можно разобраться
Это примеры на которых можно разобраться
 Учись на отлично с библиотекой
Учись на отлично с библиотекой