Установить, что 3 плоскости имеют общую точку и вычислить ее координаты с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
«Установить, что 3 плоскости имеют общую точку и вычислить ее координаты с помощью матричного исчисления, методом Гаусса и по формуле Крамера.»
- Высшая математика
Условие:
Установить, что 3 плоскости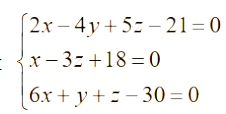 
имеют общую точку и вычислить ее координаты с помощью матричного исчисления, методом Гаусса и по формуле Крамера.
Решение:
Три плоскости имеют одну общую точку тогда, когда система, составленная из уравнений этих плоскостей, имеет единственное решение. Система имеет единственное решение, если определитель не равен нулю.
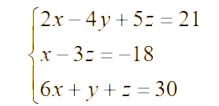
Найдем определитель системы, разложив по элементам первой строки
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э