В предположении, что описанная социальная динамика остается неизменной на протяжении многих лет, определите финальный социальный состав жителей города.
- Высшая математика
Условие:
Каждый житель некоторого города принадлежит к одной из социальных групп (богатые, средний класс, живущие за чертой бедности). По истечении года представитель i-й группы сохраняет свой социальный статус с вероятностью Pi, или с равными вероятностями переходит в одну из двух других групп. Пусть в данный момент a% жителей богаты, b% относятся к среднему классу, c% живут в нищете. В предположении, что описанная социальная динамика остается неизменной на протяжении многих лет, определите финальный социальный состав жителей города.
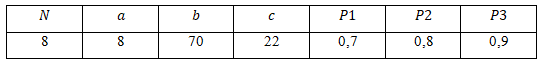
Решение:
Составляем матрицу переходом для описанного марковского процесса:
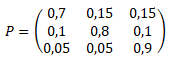
Определим финальные вероятности пребывания системы во всех состояниях. Записываем систему алгебраических уравнений для нахождения финальных вероятностей: в левой части системы вектор неизвестных вероятностей, в правой части транспонированная матрица переходов за один шаг. Кроме того, дополняем систему нормировочным уравнением. Имее...
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства