1. Главная
  2. Библиотека
  3. Высшая математика
  4. В результате производства и реализации единицы продукции A один, А два , А три завод получает чистый доход, зависящий от с...

В результате производства и реализации единицы продукции A один, А два , А три завод получает чистый доход, зависящий от спроса на продукцию, который может принимать одно из состояний В один, В два, В три, В четыре, заранее неизвестно какое именно.

«В результате производства и реализации единицы продукции A один, А два , А три завод получает чистый доход, зависящий от спроса на продукцию, который может принимать одно из состояний В один, В два, В три, В четыре, заранее неизвестно какое именно.»
  • Высшая математика

Условие:

В результате производства и реализации единицы продукции А1, А2, А3 завод получает чистый доход, зависящий от спроса на продукцию, который может принимать одно из состояний В1, В2, В3, В4, заранее неизвестно какое именно. Возможные значения дохода представлены платёжной матрицей.

 

Таблица 1 – Платёжная матрица

1. Произвести упрощение платёжной матрицы, используя принцип доминирования.

2. Найти оптимальные стратегии игроков и цену игры, используя классические критерии: ММ (Вальда), Н (оптимизма); N (нейтральный); S (Сэвиджа).

3. В каких пропорциях следует выпускать продукцию А1, А2, А3, чтобы гарантировать максимальный чистый доход при любом состоянии спроса.

Решение:

1. Используем критерии для выбора оптимальных стратегий и нахождения цены игры:

Критерий (ММ) Вальда (рис. 1):

Так как в данном примере аij представляет чистый (выигрыш), то применятся максиминный критерий.

Для .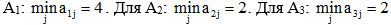

.

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я