Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.
«Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.»
- Высшая математика
Условие:
1. Вычислить определенный интеграл 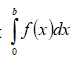 с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем почленно его проинтегрировав.
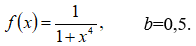
2. . Найти три первых, отличных от нуля члена разложения в степенной ряд решения
y = y(x) дифференциального уравнения 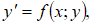 удовлетворяющего начальному условию y(0) = y0.
удовлетворяющего начальному условию y(0) = y0.
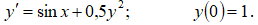
Решение:
1.
Представим подынтегральную функцию в виде степенного ряда, используя разложение в степенной ряд функции ( 1 + x4)-1. Имеем:
( 1 + x4)-1= 1 - x4 + x8 - x12 + x16 - ...
Проинтегрируем почленно данный ряд:
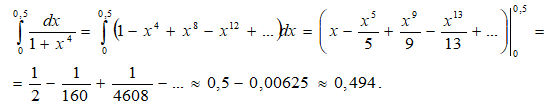
Докажем теперь, что выполнена требуемая точность.
Первый отброшенный член 1/46080,001.
Наш знакочередующийся ряд удовлетворяет условиям теоремы Лейбница....
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э