Вычислите интеграл ∫_L(e^π dz)/((z+i)^2 (z-i) ) по контурам: а) L_1:|z-1-i|=1/2; б) L_2: x^2/1+(4y^2)/9=1; в) L_3: |z-1-i|=3/2 используя интегральную формулу Коши (или вычеты).

24 января 2025
Высшая математика

Условие:

Вычислите интеграл

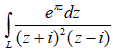
по контурам:

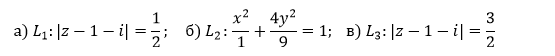
используя интегральную формулу Коши (или вычеты).

Решение:

Воспользуемся основной теоремой о вычетах:

Интеграл функции f(z) 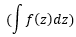взятый по замкнутому контуру L, содержащемуся в области, где функция является однозначной и аналитической, за исключением изолированных особых точек однозначного характера, и не проходящему через особые точки, равен произведению суммы вычетов функции относительно всех особых точек, заключенных внутри L, на 2i, т.е.