Решение задачи
Выполнить методом наименьших квадратов полиномиальную аппроксимацию непрерывной на отрезке функции.
- Высшая математика
Условие:
Выполнить методом наименьших квадратов полиномиальную аппроксимацию непрерывной на отрезке функции.
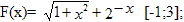
Решение:
Выполняем в Ms Excel.
Сначала нам необходимо разбить данный отрезок при помощи "Чебышевского" разбиения, т.к. данный вид разбиения всегда дает более точный результат.
В колонке I(рис. 1) записываем числа от 0 до 8, т.к. отрезок разбиваем на 8 частей.
В колонке z ячейки вычисляем по формуле: -COS(3,141593*I/8). Для вычисления каждой ячейки используем соответствующее ей I.
Значение каждого x находим по формуле: 2*z + 1.
В колонке F(x) вычисляем значение данной функции для каждого x.
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
S
А
Б
В
Г
И
К
М
П
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
Р
С
Т
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства
Ф
Э