Задан закон распределения двумерного дискретного случайного вектора {X; Y} . Найти: 1) маргинальные законы распределения его компонент X и Y; 2) функции распределения случайных величин X и Y; 3) функцию их совместного распределения;
- Высшая математика
Условие:
Задан закон распределения двумерного дискретного случайного вектора {X; Y} . Найти: 1) маргинальные законы распределения его компонент X и Y; 2) функции распределения случайных величин X и Y; 3) функцию их совместного распределения; 4) условные законы распределения случайной величины X при условии Y = yj и условные законы распределения случайной величины Y при условии X = xi , i = 1, ..., n; 5) числовые характеристики случайных величин X и Y; 6) функции регрессии Y на X и X на Y. Построить линии регрессии. Выяснить, являются ли случайные величины X и Y независимыми.

Решение:
1) маргинальные законы распределения его компонент X и Y
Случайная величина принимает значения 0, 1, 2. Вероятности, с которыми X принимает эти значения определим, суммируя соответствующие столбцы исходной таблицы
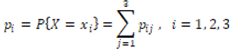
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
AI помощники
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства