1. Главная
  2. Библиотека
  3. Автоматика и управление
  4. Дискретная случайная величина Х принимает значения х1, х2, х3, свероятностями р1, р2, р3 соответственно (табл.1.2).1) Нари...

Дискретная случайная величина Х принимает значения х1, х2, х3, свероятностями р1, р2, р3 соответственно (табл.1.2).1) Нарисовать график функции распределения дискретной случайнойвеличины Х.2) Вычислить математическое ожидание, дисперсию, второй

«Дискретная случайная величина Х принимает значения х1, х2, х3, свероятностями р1, р2, р3 соответственно (табл.1.2).1) Нарисовать график функции распределения дискретной случайнойвеличины Х.2) Вычислить математическое ожидание, дисперсию, второй»
  • Автоматика и управление

Условие:

Дискретная случайная величина Х принимает значения х1, х2, х3, с
вероятностями р1, р2, р3 соответственно (табл.1.2).
1) Нарисовать график функции распределения дискретной случайной
величины Х.
2) Вычислить математическое ожидание, дисперсию, второй начальный
момент, среднеквадратическое отклонение и коэффициент вариации
случайной величины Х.

Функция распределения F(X).
F(x≤1) = 0
F(1< x ≤5) = 0.5
F(5< x ≤10) = 0.4 + 0.5 = 0.9
F(x>10) = 1

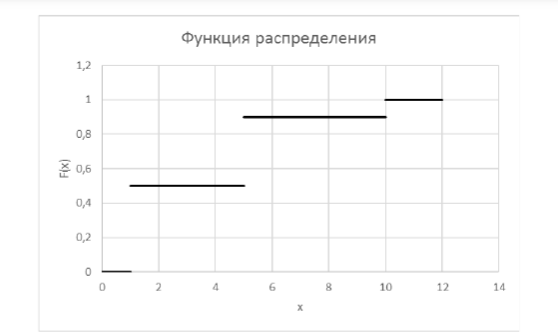
Рис. 2 График функции раcпределения

 

Решение:

Математическое ожидание находим по формуле m = xipi.Математическое ожидание M[X].M[x] = 1*0.5 + 5*0.4 + 10*0.1 = 3.5Второй ...

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я