Условие:
Определить сигнал X2(t) на выходе системы, если входной сигнал описывается уравнением вида:
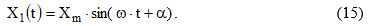
а передаточная функция системы описывается выражением вида:

Построить зависимость выходного сигнала X2(t) от входного X1(t) (график X2(t)=f(X1(t)) ) за период.
Исходные данные: Xm=6; ω=60 рад/с; А=38; α=700 ; В=0,6.
Решение:
При гармоническом входном воздействии в устойчивых системах после окончания переходного процесса выходная переменная также изменяется по гармоническому закону с той же частотой, но с другой амплитудой и фазой. Амплитуда равна амплитуде входного сигнала, умноженной на модуль частотной передаточной функции |W(j)| , а сдвиг фазы ее аргументу argW(j) . Поэтому если система с передаточной функцией W(j) устойчива, то после окончания переходного процесса выходной сигнал имеет вид:
