Условие задачи
Работа некоторого устройства характеризуется графом, представленным на рисунке 1.
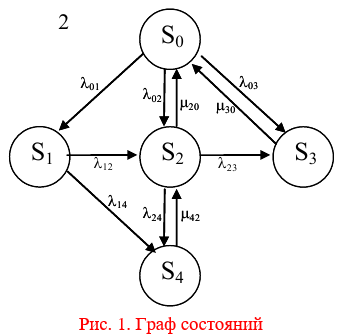
Должно быть:
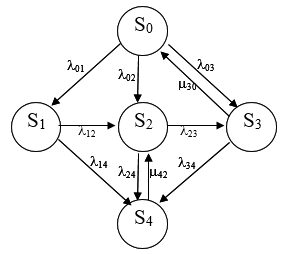
При этом S0 – исправное состояние, S1, S2, S3 – работоспособные состояния с различными неисправностями, S4 – неработоспособное состояние (состояние отказа). Вероятности переходов между состояниями характеризуются интенсивностями отказов 𝝀ik и интенсивностями восстановления μki.
Исходя из заданных значений интенсивностей отказов 𝝀ik и интенсивностей восстановления μki, найти параметры надежности (предполагая простейший поток отказов):
1) финальные вероятности нахождения системы во всех состояниях, в том числе вероятность отказа системы Qс;
2) среднее время наработки на отказ Тср и интенсивность отказов системы 𝝀с;
3) среднее время восстановления Тв;
4) коэффициент готовности Кг;
5) среднее время безотказной работы (среднюю наработку до отказа) Тот.
Выбор численных параметров
𝜆ik=𝜆=n*10-41/ч ;
µik=µ=10/n1/ч ,
где n – номер варианта задания.
Для варианта №5:
𝜆ik=𝜆 =5*10-4=0,005 1/ч ;
µik=µ=10/5=2 1/ч .
Ответ
Исходя из графа, система может находиться в одном из 5 состояний:
0 исправное состояние;
1 1-е работоспособное состояние: отказал первый элемент (находится в ремонте), второй, третий исправен;
2 2-е работоспособное состояние: отказал второй элемент (находится в ремонте), первый, третий исправен;
3 3-е работоспособное состояние: отказал третий элемент (находится в ремонте), первый, второй исправен;
4 неработоспособное состояние (состояние отказа): отказали последовательно три элемента и находятся в состоянии ремонта.
Систему дифференциальных уравнений можно записать в виде:
