Используя узлы интерполяции построить аппроксимирующие полиномы второго порядка методом наименьших квадратов при всех одинаковых весовых коэффициентах и при весовом коэффициенте в третьей точке в 3 раза большем, чем в остальных.
- Автоматизация технологических процессов
Условие:
Используя заданные узлы интерполяции построить аппроксимирующие полиномы второго порядка у = a2х2 + a1x + a0 ме¬тодом наименьших квадратов при всех одинаковых весовых коэффициен¬тах и при весовом коэффициенте в третьей точке в 3 раза большем, чем в остальных (т.е. при β3=3). Получить среднеквадратичную погрешность аппроксимации, величину квадратичного критерия близости и расчётное значение y в третьей точке. Сравнить полученные результаты. Сделать выводы о том, устраивает ли полученное аппроксимирующее уравнение второго порядка по погрешности, сравнивая среднеквадратичную погрешность с заданной погрешностью в обоих случаях, т.е. и при всех одинаковых весовых коэффициентах и при β3=3. Если результат не устраивает, то наметить путь, что делать в таком случае дальше. Также проанализировать, как повлияло введение весового коэффициента β3=3 на точность аппроксимации в третьей точке (по величине абсолютной погрешности в этой точке) и на точность аппроксимации в целом, (по величине критерия близости).
Решение:
Заданная функция f(x)=-1*1.5x + sin(4x+2); интервал [-10;5/4]
Таблица 3 узлы интерполяции
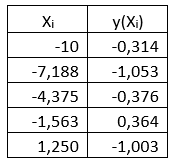
Определение аппроксимирующей функции при помощи метода наименьших квадратов для равных весовых коэффициентов
В общем случае квадратичный критерий близости равен (1):
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства