Условие:
Изучалась зависимость между двумя признаками X и Y. Выполните анализ характера распределения значений данных признаков:
1. Вычислить числовые характеристики: среднее значение и показатели вариации по исходным (не сгруппированным) данным. Сделать выводы о степени вариации и однородности совокупности наблюдений.
2. Для признака Х построить интервальный ряд распределения (разбить на 3 интервала), изобразить полученное распределение графически (гистограмма и полигон распределения). Вычислить обобщающие числовые характеристики по сгруппированным данным. Сравнить результаты расчетов с предыдущими результатами, сделать вывод.
3. Для признака Y построить дискретный ряд распределения, изобразить полученное распределение графически (полигон и кумулята распределения). Вычислить обобщающие числовые характеристики по сгруппированным данным. Сравнить результаты расчетов с предыдущими результатами, сделать вывод.
4. Для обоих признаков выполнить интервальную оценку средних значений с надежностью 0,997.
5. Для обоих признаков выполнить интервальную оценку доли единиц наблюдения со значениями признака выше полученного среднего по выборке, приняв надежность оценки 0,954.
Решение:
1. Расчет числовых характеристик по несгруппированным исходным данным.
Среднее значение 
Размах вариации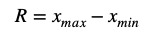 
Выборочная дисперсия