![Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3 [(N - 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля,](/public/images/library/external/library-detail-hero-book.png)
Условие:
Специализированный пост диагностики представляет собой одноканальную СМО.
Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3 [(N - 1) = 3]. Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность λ = 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час.
Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Решение:
1. Параметр потока обслуживании автомобилей:
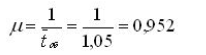
2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей и , т. е.
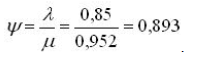
3. Вычислим финальные вероятности системы: