Условие:
Фирма производит и продает два типа товаров. Фирма получает прибыль в размере c1 = 11 тыс. р. от производства и продажи каждой единицы товара 1 и в размере c2 = 5 тыс. р. от производства и продажи каждой единицы товара 2. Фирма состоит из трех подразделений. Затраты труда (человеко-дни) на производство этих товаров в каждом из подразделений указаны в таблице.
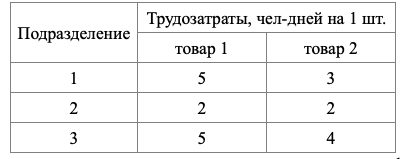
Руководство рассчитало, что в следующем месяце фирма будет располагать следующими возможностями обеспечения производства трудозатратами: D1 = 1000 чел-дней в подразделении 1, D2 = 600 – в подразделении 2 и D3 = 1900 – в подразделении 3.
Составить задачу линейного программирования и найти ее решение.
Решение:
Составляем математическую модель нашей задачи.
Обозначаем количества производимых и продаваемых товаров:
x1 количество производимых и продаваемых товаров 1 (штук);
x2 количество производимых и продаваемых товаров 2 (штук).
При этом прибыль фирмы составляет F = 11x1 + 5x2 тыс. р.
Целью решения задачи является определение среди всех допустимых таких значений x1 и x2, которые обеспечивают наибольшую прибыль.
Рассмотрим ограничения задачи.
Количества производимых и продаваемых товаров не могут быть отрицательными, поэтому x1 0, x2 0. Кроме того, по смыслу задачи, x1 и x2 целочисленные.
Другие огранич...
