1. Главная
  2. Библиотека
  3. Эконометрика
  4. Графический метод. Задача об использовании ресурсов. Для производства изделий вида А и В используются 3 вида сырья. На изг...

Графический метод. Задача об использовании ресурсов. Для производства изделий вида А и В используются 3 вида сырья. На изготовление единицы изделия А требуется сырья первого вида А1

«Графический метод. Задача об использовании ресурсов. Для производства изделий вида А и В используются 3 вида сырья. На изготовление единицы изделия А требуется сырья первого вида А1»
  • Эконометрика

Условие:

Задача об использовании ресурсов. Решить графическим методом.

Для производства изделий вида А и В используются 3 вида сырья. На изготовление единицы изделия А требуется сырья первого вида А1 , второго вида А2, третьего вида А3. На изготовление единицы изделия В требуется сырья первого вида В1 , второго В2, третьего В3. Производство обеспечено сырьем первого вида р1, второго вида р2, третьего вида р3. Прибыль от реализации единицы готовой продукции изделий А равна α изделий В равна β. Составить план производства изделий А и В, обеспечивающий максимальную прибыль.

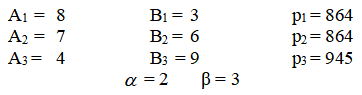
Решение:

Обозначим через х1 и х2 количество произведенных изделий вида А и В соответственно.

Необходимо найти максимальное значение целевой функции

F = 2x1+3x2 max,

при системе ограничений:

8x1+3x2 864, (1)

7x1+6x2 864, (2)

4x1+9x2 945, (3)

x1 0, (4)

x2 0, (5)

Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Похожие задачи

Не нашел нужную задачу?

Воспользуйся поиском

AI помощники

Выбери предмет

E
S
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Э
Я