Условие задачи
На основании представленных ниже данных:
1. Определить параметры уравнения линейной множественной регрессии по методу наименьших квадратов. Дать экономическую интерпретацию параметрам уравнения.
2. Рассчитать парные коэффициенты корреляции.
3.Определить коэффициенты множественной корреляции и детерминации. Сделать вывод о тесноте связи результата с факторами и объясняемое вариации результата.
4. Оцепить значимость уравнения множественной регрессии с помощью F- критерия Фишера при уровнях значимости α = 0,05 и α = 0,01. Сделать вывод.
5. Получить уравнение регрессии в стандартизованном масштабе. Дать экономическую интерпретацию параметрам уравнения. Оценить информативность факторов на основе уравнения линейной регрессии в стандартизированном масштабе.
6. Рассчитать индексы множественной корреляции и детерминации для линейного уравнения регрессии в стандартизованном масштабе.
7. Проверить гипотезу о гомоскедастичности ряда остатков с уровнем значимости α = 0,05 (тест Голдфелда и Куандта).
8. Вычислить определитель матрицы межфакторной корреляции. Сделать вывод о взаимной коррелированности объясняющих переменных.
9. Выбрать наиболее значимый фактор.
10. Вычислить оценки коэффициентов однофакторной линейной модели (в качестве фактора принять наиболее значимый фактор) по методу наименьших квадратов. Дать экономическую интерпретацию коэффициента регрессии.
11. Определить коэффициенты корреляции и детерминации. Сделать вывод о тесноте связи результата с фактором и объясняемости вариации результата.
12. Рассчитать факторную, остаточную и общую дисперсии на одну степень свободы.
13. Оценить значимость уравнения линейной регрессии с помощью F – критерия Фишера при уровнях значимости α = 0,05 и α = 0,01. Сделать вывод.
14. Определить стандартную ошибку коэффициента регрессии, оценить его значимость.
15. Найти доверительный интервал для коэффициента регрессии.
16. Определить стандартную ошибку параметра а, оценить его значимость.
17. Найти доверительный интервал для параметра а.
18. Сделать вывод о значимости линейного коэффициента корреляции.
| № предприятия | |||
| Товарооборот за месяц (y) тыс.руб. | Площадь торгового зала (x1)? кв.м. | Затраты на содержание торговой точки (х2) тыс.руб. | |
| 1 | 680,0 | 7,5 | 96,0 |
| 2 | 755,6 | 8,8 | 100,6 |
| 3 | 811,7 | 9,8 | 124,3 |
| 4 | 880,0 | 14,1 | 118,8 |
| 5 | 1041,8 | 14,9 | 138,2 |
| 6 | 1142,1 | 15,9 | 131,4 |
| 7 | 1299,2 | 17,3 | 271,3 |
| 8 | 1416,4 | 27,7 | 206,6 |
| 9 | 1543,6 | 25,3 | 311,0 |
| 10 | 1593,8 | 27,1 | 322,4 |
| 11 | 1668,2 | 28,6 | 352,2 |
| 12 | 1747,6 | 32,5 | 397,3 |
| 13 | 1892,1 | 35,4 | 440,3 |
| 14 | 1950,1 | 38,8 | 424,7 |
| 15 | 2047,6 | 40,2 | 470,8 |
| 16 | 2099,9 | 48,2 | 461,5 |
| 17 | 2281,0 | 44,8 | 546,6 |
| 18 | 2581,3 | 51,6 | 455,4 |
| 19 | 2859,0 | 58,7 | 661,6 |
| 20 | 2961,7 | 72,5 | 744,5 |
Ответ
В нашем случае зависимость товарооборота за месяц характеризуется следующим уравнением
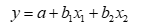
Параметры уравнения множественной регрессии оцениваются методом наименьших квадратов. Система нормальных уравнений имеет вид:
