Предположим, что Вы инвестируете долю W Ваших свободных средств в портфель акций и остальные средства - в портфель облигаций. При каком значении W риск Ваших вложений будет минимальным?
- Эконометрика
Условие:
Предположим, что Вы инвестируете долю W Ваших свободных средств в портфель акций и остальные средства (1 – W) в портфель облигаций. Пусть R_1 – доходность портфеля акций: случайная величина со средним значением 15,5% и стандартным отклонением 4,9%; и R_2 – доходность портфеля облигаций: случайная величина со средним значением 10,7% и стандартным отклонением 4%. Корреляция между R_1 и R_2 равна 0,423.
1) При каком значении W риск (дисперсия) Ваших вложений будет минимальным?
2) Постройте 90% доверительный интервал для значения доходности такого портфеля, который соответствует полученному минимальному риску.
Решение:
1) Дисперсия портфеля:
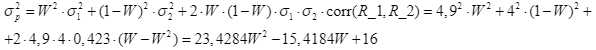
Минимизируем функцию риска. Для этого найдем ее производную и приравняем к нулю:
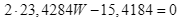
Откуда доля акций в портфеле W=0.3291.
При этом оптимальные доходность и риск составят:
Похожие задачи
Не нашел нужную задачу?
Воспользуйся поиском
Выбери предмет
- Правоохранительные органы
- Пожарная безопасность
- Парикмахерское искусство
- Природообустройство и водопользование
- Почвоведение
- Приборостроение и оптотехника
- Промышленный маркетинг и менеджмент
- Производственный маркетинг и менеджмент
- Процессы и аппараты
- Программирование
- Право и юриспруденция
- Психология
- Политология
- Педагогика
- Трудовое право
- Теория государства и права (ТГП)
- Таможенное право
- Теория игр
- Текстильная промышленность
- Теория вероятностей
- Теоретическая механика
- Теория управления
- Технология продовольственных продуктов и товаров
- Технологические машины и оборудование
- Теплоэнергетика и теплотехника
- Туризм
- Товароведение
- Таможенное дело
- Торговое дело
- Теория машин и механизмов
- Транспортные средства