Условие задачи
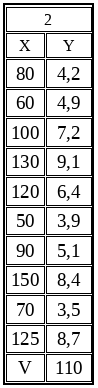
При изучении зависимости издержек обращения Y (млн. руб.) от объема товарооборота X (млн. руб.) было обследовано 10 однотипных фирм и получены следующие данные (табл. 1,2 по вариантам). Считая, что между признаками Y и X имеет место линейная корреляционная связь, требуется:
1. Получить линейное уравнение парной регрессии у(х).
2. Построить диаграмму рассеяния и линию регрессии.
3. Используя полученную связь, определить ожидаемую величину издержек обращения при объеме товарооборота V млн. руб. (см. табл. 1,2).
4. Рассчитать линейный коэффициент парной корреляции и сделать вывод о направлении и тесноте связи между признаками X и Y.
5. Определить коэффициент детерминации и выявить долю вариации (%),
объясняемую линейной регрессией.
6. Рассчитать среднюю ошибку аппроксимации.
7. Найти доверительные интервалы для параметров регрессии с надежностью γ = 0,95.
8. Определить статистическую значимость уравнения регрессии с
использованием дисперсионного анализа с применением критерия
Фишера.
9. С помощью фиктивных переменных по качественному признаку
«использование новых технологий» получить уравнения регрессии и дать
экономическую интерпретацию.
Таблица 1.
Ответ
1. Получить линейное уравнение парной регрессии у(х).
В общем виде однофакторная линейная эконометрическая модель записывается следующим образом: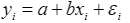 
где y - вектор наблюдений за результативным показателем;
x - вектор наблюдений за фактором;
a, b - неизвестные параметры, что подлежат определению;
i - случайная величина (отклонение, остаток)
Ее оценкой является модель:
